공분산, 상관계수, 결정계수 특징 정리와 파이썬 코드
Programming/Extractions 2021. 4. 28. 12:36공분산은 2개 확률변수의 상관 정도를 나타내는데, 평균 편차의 곱으로 구할 수 있다.
수식은 대충 아래와 같다.
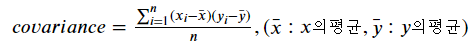
계산 결과 두 변수의 covariance가 0보다 크면 x와 y가 비례 관계, 0보다 작으면 반비례 관계이다. 0이면 변수 간 아무 선형관계가 없어 서로 독립 관계라고 할 수 있다.
공분산의 문제는 단위에 영향을 받는다는 것. 예를 들어, 어떤 시험의 만점이 10점인 경우에는 작게, 100점인 경우에는 큰 결과값이 나타난다. 이것 때문에 상관계수(correlation coefficient)가 있다. 상관계수는 공분산을 두 분산의 곱의 제곱근으로 나누어 구할 수 있다.
상관계수의 절대값은 1을 넘지 못하고, 두 변수가 독립이면 상관계수는 0이다. 선형적 관계에서 상관계수는 1~-1의 범위 내에서 나타나고, 1과 가까울수록 양의 선형관계, -1에 가까울수록 음의 선형관계이다.
상관계수의 음수따윈 모르겠고, 상관관계가 좀더 확실한 놈들을 눈여겨 보기 위해서서 결정계수(coefficient of determination)를 이용한다. 즉, 결정계수는 상관계수를 제곱하여 상관관계가 큰 녀석들을 독보적으로 나타낸다.
파이썬에서는 이것들을 NumPy를 이용한다. 아니, 이용해야 한다. NumPy는 내부적으로 C, C++ 등의 네이티브 언어로 되어 있는데, 파이썬으로 작성해서 이러한 통계치를 직접 구했을 때와 비교하면 속도 차이가 실로 어마어마하다(!!)
import numpy as np
p_data1 = np.random.randint(60, 100, int(1E5))
p_data2 = np.random.randint(60, 100, int(1E5))
np.var(p_data1), np.var(p_data2) # 분산
np.cov(p_data1, p_data2)[0, 1] # 공분산
np.corrcoef(data1, data2)[0,1] # 상관계수
np.corrcoef(data1, data2)[0,1] ** 2 # 결정계수'Programming > Extractions' 카테고리의 다른 글
| 원격 프로시저 호출(Remote Procedure Call, RPC) (0) | 2021.04.14 |
|---|---|
| 메시지 지향 미들웨어(Message Oriented Middleware, MOM) (0) | 2021.04.14 |
| Call by Reference, Call by Value에 대한 고찰 (0) | 2021.02.11 |
| CNN 용어 정리 (0) | 2021.01.28 |
| RNN 학습에 필요한 데이터 분할 (0) | 2021.01.25 |






